Using External Networks (and external packages)

Although {EGAnet} features many common methods used in the network psychometric literature, it does not include all possible options. Sometimes you might switch between {EGAnet} and other packages.

Alternative Networks

There are many different packages available to estimate psychometric networks. One common package is {bootnet}. bootnet::estimateNetwork offers many different methods to estimate networks. The "ggmModSelect" approach will be used as an example.

# Load packages
library(EGAnet); library(bootnet)

# Load data
data <- wmt2[,7:24]

# Estimate network
stepwise_result <- estimateNetwork(
  data = data, default = "ggmModSelect", stepwise = TRUE
)

Once a network is estimated, then a modular approach to estimating the EGA workflow can be used. This workflow is the same as what’s used internally in the EGA function. If the network is coming from an {igraph} must be converted using the igraph2matrix function (e.g., ega_network <- igraph2matrix(igraph_network)). Any network that is a matrix or data frame object can be used in {EGAnet} functions like the output from estimateNetwork.

Check for Unidimensionality

# Perform unidimensionality check
unidimensional_membership <- community.unidimensional(data)

# Print
unidimensional_membership

Algorithm:  Louvain

Number of communities:  2

 wmt1  wmt2  wmt3  wmt4  wmt5  wmt6  wmt7  wmt8  wmt9 wmt10 wmt11 wmt12 wmt13 
    1     1     1     1     1     2     2     2     2     1     2     2     2 
wmt14 wmt15 wmt16 wmt17 wmt18 
    2     2     2     2     2 

The standard unidimensional check uses the Louvain Louvain algorithm on the zero-order correlation matrix (Christensen, 2023). The output will include the memberships regardless of whether the data are detected as unidimensional. In this output, the number of communities is 2 and therefore not unidimensional. If the number of communities was 1, then there is no need to proceed with the multidimensional estimation.

Estimate Multidimensionality

# Estimate multidimensionality
multidimensional_membership <- community.detection(
  stepwise_result$graph, algorithm = "walktrap"
)

# Print
multidimensional_membership

Algorithm:  Walktrap

Number of communities:  2

 wmt1  wmt2  wmt3  wmt4  wmt5  wmt6  wmt7  wmt8  wmt9 wmt10 wmt11 wmt12 wmt13 
    1     1     1     1     1     1     2     2     2     1     2     2     2 
wmt14 wmt15 wmt16 wmt17 wmt18 
    2     2     2     2     2 

For the multidimensional estimation, the estimated network should be used as the input. The algorithm can be set using a number of different algorithms (see ?community.detection) but the default is to use the Walktrap algorithm. From this output, Walktrap estimates 2 communities.

Obtain Final Memberships

A shortcut to obtain the final memberships as is used in EGA is provided below:

wc <- EGAnet:::swiftelse(
    # Check for whether unidimensional membership should be used
    EGAnet:::unique_length(unidimensional_membership) == 1,
    unidimensional_membership, multidimensional_membership
    # Otherwise, use multidimensional membership
  )

Plot

In order to plot using {EGAnet}, the network and memberships need to be set up as an EGA class object:

# Set up EGA object
ega_object <- list(
  network = stepwise_result$graph,
  wc = wc
)

# Set `EGA` class
class(ega_object) <- "EGA"

# Plot
plot(ega_object)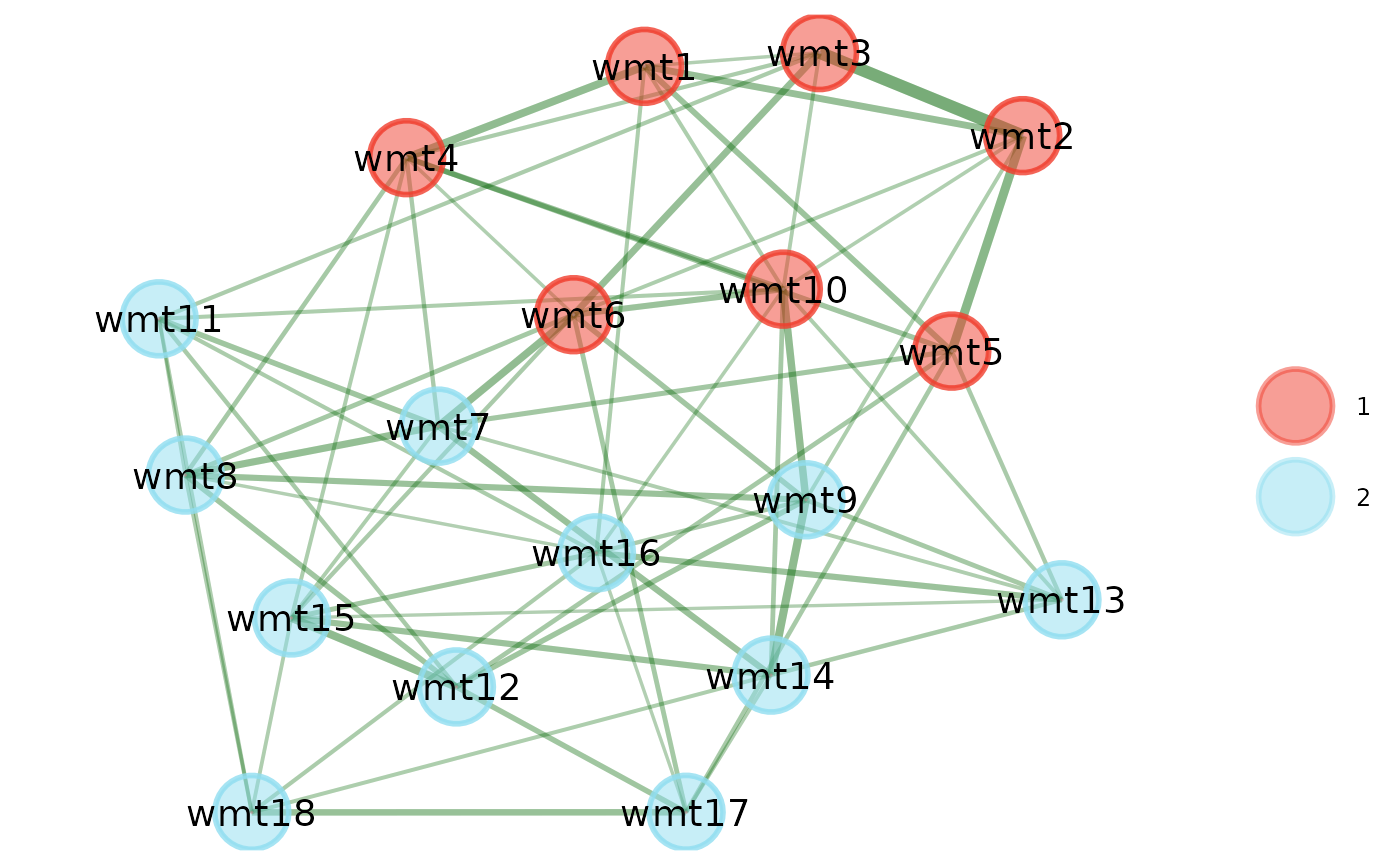

Modularity

Modularity can also be computed using the estimated network and appropriate memberships.

modularity(stepwise_result$graph, wc)

[1] 0.204308

Alternative Similarity Measures

By default, {EGAnet} uses the auto.correlate function to compute appropriate correlations for each set of pairwise variables. Other measures might need to be used in {EGAnet} functions.

Cosine Similarity

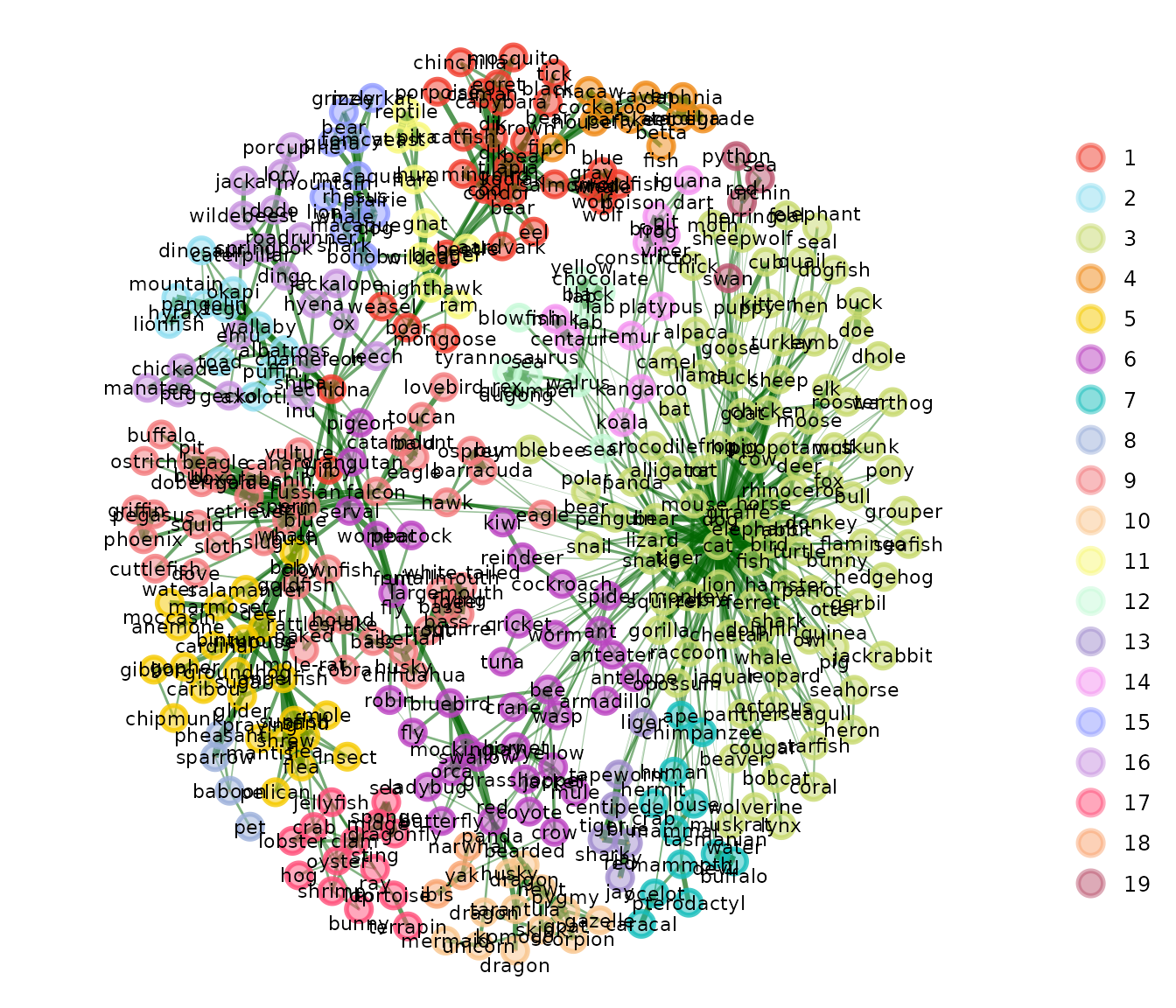
A common example is from natural language processing and cognitive science where cosine similarity is a common association measure between two terms. Below, we’ll show a semantic network example from the {SemNeT} package.

# Load packages
library(EGAnet); library(SemNeT)

# Compute cosine similarity
animals_cosine <- similarity(open.binary, method = "cosine")

This data are from participants who performed a verbal fluency task and generated animals for 1 minute. Each row represents a participant and each column represents an animal. A 1 is an animal a participant provided; a 0 is an animal a participant did not provide.

The animals_cosine object is a symmetric matrix that represents the cosine similarity between each animal. To use the cosine similarity matrix (or any other alternative similarity matrix) in an {EGAnet} function, n or the number of cases must be set:

# Compute EGA
animals_ega <- EGA(
  # Arguments for `EGA`
  animals_cosine, n = nrow(open.binary), model = "TMFG",
  # Arguments for `plot`
  node.size = 4, label.size = 3, edge.size = 2
)