Dimension Stability Statistics from bootEGA

Based on the bootEGA results, this function computes the stability of dimensions. Stability is computed by assessing the proportion of times the original dimension is exactly replicated in across bootstrap samples

Usage

dimensionStability(bootega.obj, IS.plot = TRUE, structure = NULL, ...)

Arguments

bootega.obj

A bootEGA object

IS.plot

Boolean (length = 1). Should the plot be produced for item.replication? Defaults to TRUE

structure

Numeric (length = number of variables). A theoretical or pre-defined structure. Defaults to NULL or the empirical EGA result in the bootega.obj

...

Additional arguments. Used for deprecated arguments from previous versions of itemStability

Value

Returns a list containing:

dimension.stability

A list containing:

• structural.consistency — The proportion of times that each empirical EGA dimension exactly replicates across the bootEGA samples

• average.item.stability — The average item stability in each empirical EGA dimension

item.stability

Results from itemStability

References

Original implementation of bootEGA
Christensen, A. P., & Golino, H. (2021). Estimating the stability of the number of factors via Bootstrap Exploratory Graph Analysis: A tutorial. Psych, 3(3), 479-500.

Conceptual introduction
Christensen, A. P., Golino, H., & Silvia, P. J. (2020). A psychometric network perspective on the validity and validation of personality trait questionnaires. European Journal of Personality, 34(6), 1095-1108.

Author

Hudson Golino <hfg9s at virginia.edu> and Alexander P. Christensen <alexpaulchristensen@gmail.com>

Examples

# Load data
wmt <- wmt2[,7:24]

if (FALSE) { # \dontrun{
# Estimate bootstrap EGA
boot.wmt <- bootEGA(
  data = wmt, iter = 500,
  type = "parametric", ncores = 2
)} # }

# Estimate stability statistics
dimensionStability(boot.wmt)

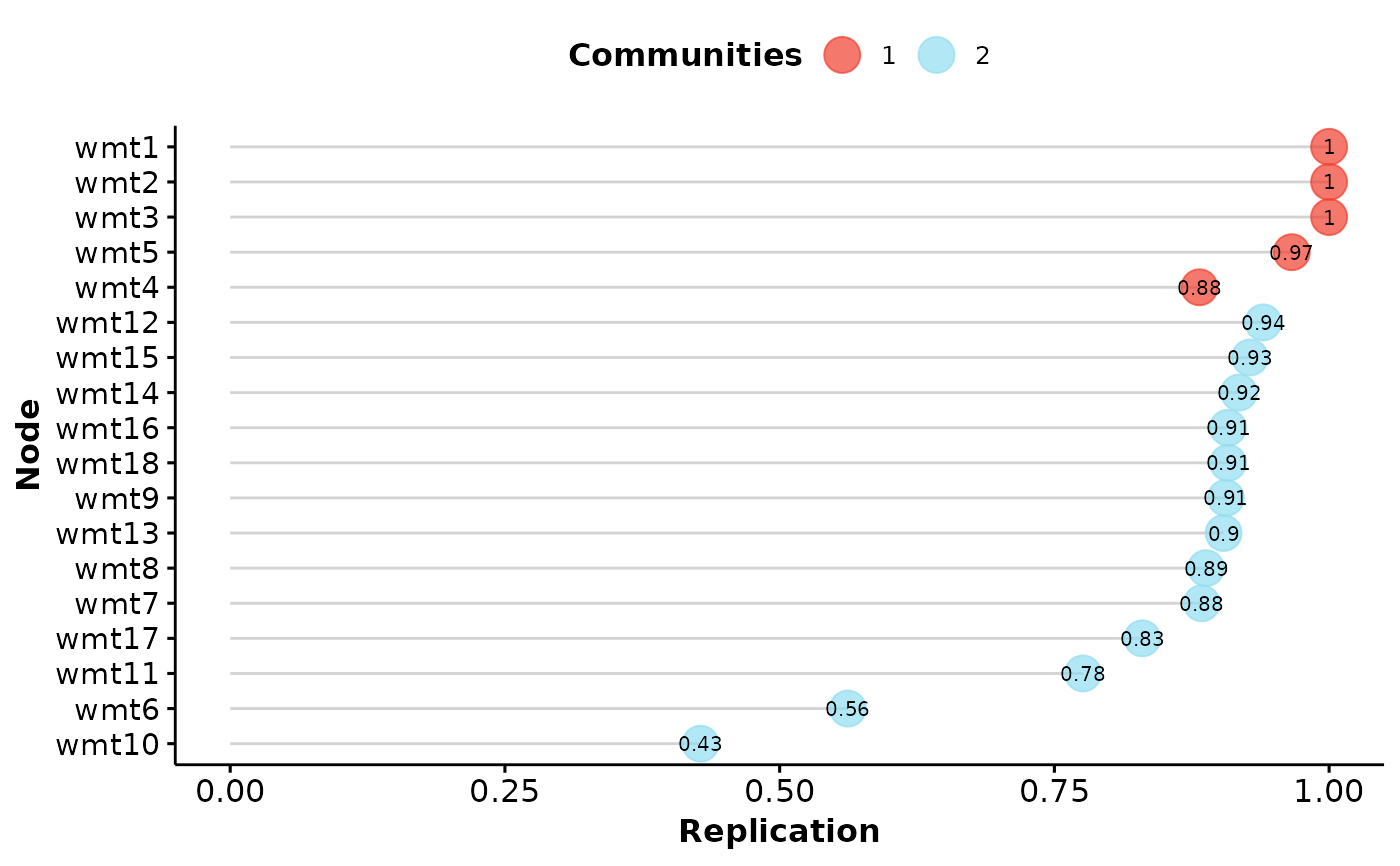#> EGA Type: EGA 
#> Bootstrap Samples: 500 (Parametric)
#> 
#> Proportion Replicated in Dimensions:
#> 
#>  wmt1  wmt2  wmt3  wmt4  wmt5  wmt6  wmt7  wmt8  wmt9 wmt10 wmt11 wmt12 wmt13 
#> 1.000 1.000 1.000 0.882 0.966 0.562 0.884 0.888 0.906 0.428 0.776 0.940 0.904 
#> wmt14 wmt15 wmt16 wmt17 wmt18 
#> 0.918 0.928 0.908 0.830 0.908 
#> 
#> ----
#> 
#> Structural Consistency:
#> 
#>     1     2 
#> 0.860 0.356