Skip to contents

Hierarchical EGA

Source: R/hierEGA.R
hierEGA.Rd

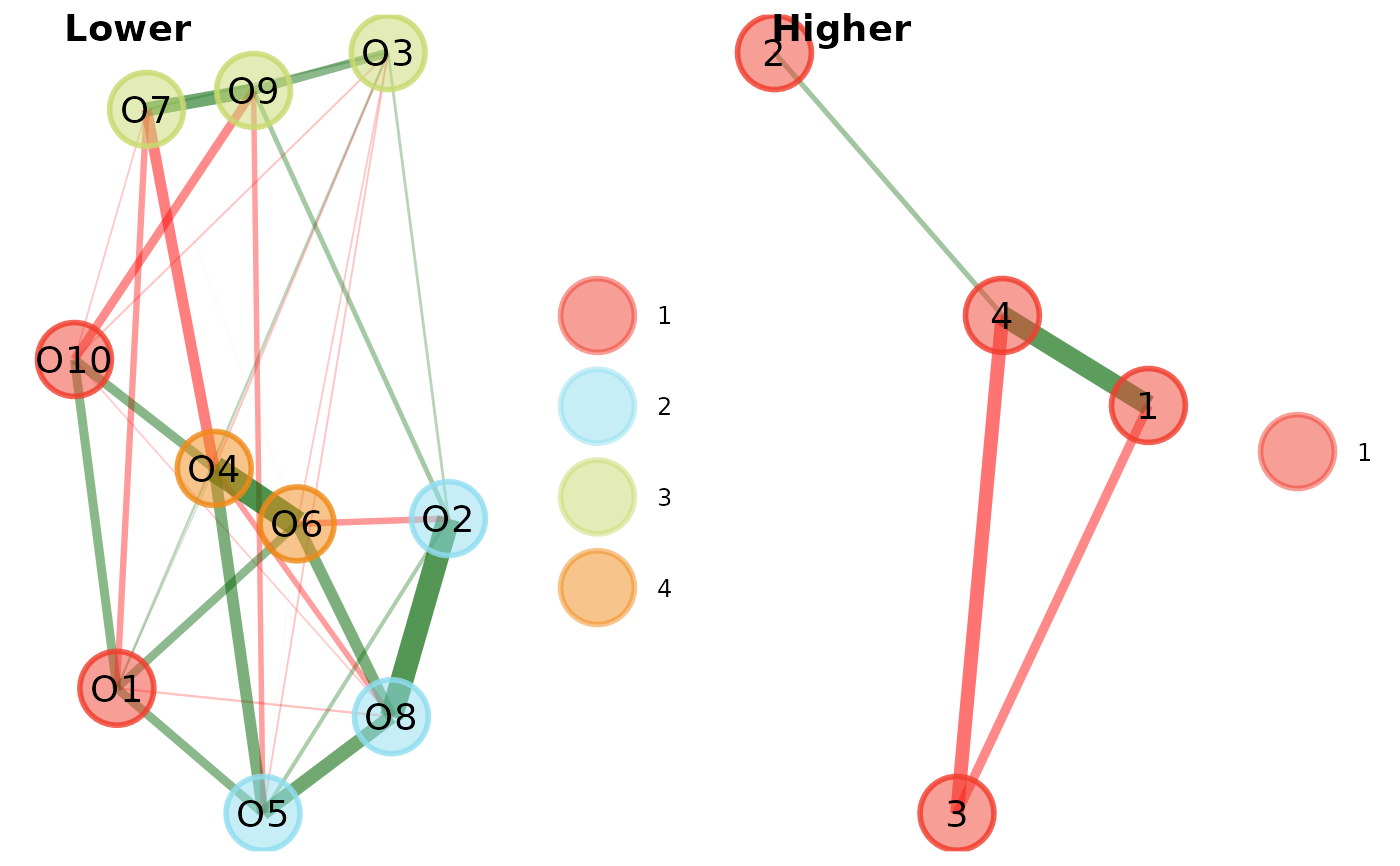
Estimates EGA using the lower-order solution of the Louvain algorithm (cluster_louvain)to identify the lower-order dimensions and then uses factor or network loadings to estimate factor or network scores, which are used to estimate the higher-order dimensions (for more details, see Jiménez et al., 2023)

Usage

hierEGA(
  data,
  loading.method = c("original", "revised"),
  rotation = NULL,
  scores = c("factor", "network"),
  loading.structure = c("simple", "full"),
  impute = c("mean", "median", "none"),
  corr = c("auto", "cor_auto", "pearson", "spearman"),
  na.data = c("pairwise", "listwise"),
  model = c("BGGM", "glasso", "TMFG"),
  lower.algorithm = "louvain",
  higher.algorithm = c("leiden", "louvain", "walktrap"),
  uni.method = c("expand", "LE", "louvain"),
  plot.EGA = TRUE,
  verbose = FALSE,
  ...
)

Arguments

data

Matrix or data frame. Should consist only of variables to be used in the analysis (does not accept correlation matrices)

loading.method

Character (length = 1). Sets network loading calculation based on implementation described in "original" (Christensen & Golino, 2021) or the "revised" (Christensen et al., 2024) implementation. Defaults to "revised"

rotation

Character. A rotation to use to obtain a simpler structure. For a list of rotations, see rotations for options. Defaults to NULL or no rotation. By setting a rotation, scores estimation will be based on the rotated loadings rather than unrotated loadings

scores

Character (length = 1). How should scores for the higher-order structure be estimated? Defaults to "network" for network scores computed using the net.scores function. Set to "factor" for factor scores computed using fa. Factors scores will be based on EFA (as in Jiménez et al., 2023)

Factor scores use the number of communities from EGA. Estimated factor loadings may not align with these communities. The plots using factor scores will have higher order factors that may not completely map on to the lower order communities. Look at $hierarchical$higher_order$lower_loadings to determine the composition of the lower order factors.

loading.structure

Character (length = 1). Whether simple structure or the saturated loading matrix should be used when computing scores (scores = "network" only). Defaults to "simple"

"simple" structure more closely mirrors traditional hierarchical factor analytic methods such as CFA; "full" structure more closely mirrors EFA methods

Simple structure is the more conservative (established) approach and is therefore the default. Treat "full" as experimental as proper vetting and validation has not been established

impute

Character (length = 1). If there are any missing data, then imputation can be implemented. Available options:

  • "none" — Default. No imputation is performed

  • "mean" — The mean value of each variable is used to replace missing data for that variable

  • "median" — The median value of each variable is used to replace missing data for that variable

corr

Character (length = 1). Method to compute correlations. Defaults to "auto". Available options:

  • "auto" — Automatically computes appropriate correlations for the data using Pearson's for continuous, polychoric for ordinal, tetrachoric for binary, and polyserial/biserial for ordinal/binary with continuous. To change the number of categories that are considered ordinal, use ordinal.categories (see polychoric.matrix for more details)

  • "cor_auto" — Uses cor_auto to compute correlations. Arguments can be passed along to the function

  • "pearson" — Pearson's correlation is computed for all variables regardless of categories

  • "spearman" — Spearman's rank-order correlation is computed for all variables regardless of categories

For other similarity measures, compute them first and input them into data with the sample size (n)

na.data

Character (length = 1). How should missing data be handled? Defaults to "pairwise". Available options:

  • "pairwise" — Computes correlation for all available cases between two variables

  • "listwise" — Computes correlation for all complete cases in the dataset

model

Character (length = 1). Defaults to "glasso". Available options:

  • "BGGM" — Computes the Bayesian Gaussian Graphical Model. Set argument ordinal.categories to determine levels allowed for a variable to be considered ordinal. See ?BGGM::estimate for more details

  • "glasso" — Computes the GLASSO with EBIC model selection. See EBICglasso.qgraph for more details

  • "TMFG" — Computes the TMFG method. See TMFG for more details

lower.algorithm

Character or cluster_* function (length = 1). Defaults to the lower order "louvain" with most common consensus clustering (1000 iterations; see community.consensus for more details)

Louvain with consensus clustering is strongly recommended. Using any other algorithm is considered experimental as they have not been designed to capture lower order communities

higher.algorithm

Character or cluster_* function (length = 1). Defaults to "louvain". Three options are listed below but all are available (see community.detection for other options):

  • "leiden" — See cluster_leiden for more details

  • "louvain" — By default, "louvain" will implement the higher-order (order = "higher") Louvain algorithm using the consensus clustering method (see community.consensus for more information). This function will implement consensus.method = "most_common" and consensus.iter = 1000 unless specified otherwise

  • "walktrap" — See cluster_walktrap for more details

Using algorithm will set only higher.algorithm and lower.algorithm will default to Louvain with most common consensus clustering (1000 iterations)

uni.method

Character (length = 1). What unidimensionality method should be used? Defaults to "louvain". Available options:

  • "expand" — Expands the correlation matrix with four variables correlated 0.50. If number of dimension returns 2 or less in check, then the data are unidimensional; otherwise, regular EGA with no matrix expansion is used. This method was used in the Golino et al.'s (2020) Psychological Methods simulation

  • "LE" — Applies the Leading Eigenvector algorithm (cluster_leading_eigen) on the empirical correlation matrix. If the number of dimensions is 1, then the Leading Eigenvector solution is used; otherwise, regular EGA is used. This method was used in the Christensen et al.'s (2023) Behavior Research Methods simulation

  • "louvain" — Applies the Louvain algorithm (cluster_louvain) on the empirical correlation matrix. If the number of dimensions is 1, then the Louvain solution is used; otherwise, regular EGA is used. This method was validated Christensen's (2022) PsyArXiv simulation. Consensus clustering can be used by specifying either "consensus.method" or "consensus.iter"

plot.EGA

Boolean. If TRUE, returns a plot of the network and its estimated dimensions. Defaults to TRUE

verbose

Boolean (length = 1). Whether messages and (insignificant) warnings should be output. Defaults to FALSE (silent calls). Set to TRUE to see all messages and warnings for every function call

...

Additional arguments to be passed on to auto.correlate, network.estimation, community.detection, community.consensus, EGA, and rotations

Value

Returns a list of lists containing:

lower_order

EGA results for the lower order structure

higher_order

EGA results for the higher order structure

parameters

A list containing lower_loadings and lower_scores that were used to estimate scores and the higher order EGA results, respectively

dim.variables

A data frame with variable names and their lower and higher order assignments

TEFI

Generalized TEFI using tefi

plot.hierEGA

Plot output if plot.EGA = TRUE

References

Hierarchical EGA simulation
Jiménez, M., Abad, F. J., Garcia-Garzon, E., Golino, H., Christensen, A. P., & Garrido, L. E. (2023). Dimensionality assessment in bifactor structures with multiple general factors: A network psychometrics approach. Psychological Methods.

3+ level hierarchical EGA
Samo, A., Christensen, A. P., Abad, F. J., Garrido, L. E., Garcia-Garzon, E., Golino, H. & McAbee, S. T. (2023). Building the structure of personality from the bottom-up using Hierarchical Exploratory Graph Analysis. PsyArXiv.

Conceptual implementation
Golino, H., Thiyagarajan, J. A., Sadana, R., Teles, M., Christensen, A. P., & Boker, S. M. (2020). Investigating the broad domains of intrinsic capacity, functional ability and environment: An exploratory graph analysis approach for improving analytical methodologies for measuring healthy aging. PsyArXiv.

Revised network loadings
Christensen, A. P., Golino, H., Abad, F. J., & Garrido, L. E. (2024). Revised network loadings. PsyArXiv.

See also

plot.EGAnet for plot usage in

Author

Marcos Jiménez <marcosjnezhquez@gmailcom>, Francisco J. Abad <fjose.abad@uam.es>, Eduardo Garcia-Garzon <egarcia@ucjc.edu>, Hudson Golino <hfg9s@virginia.edu>, Alexander P. Christensen <alexpaulchristensen@gmail.com>, and Luis Eduardo Garrido <luisgarrido@pucmm.edu.do>

Examples

# Example using network scores
opt.hier <- hierEGA(
  data = optimism, scores = "network",
  plot.EGA = FALSE # No plot for CRAN checks
)
#> Warning: This implementation of `hierEGA` is experimental. 
#> 
#> The underlying function and/or output may change until the results have been appropriately vetted and validated.
#> The default 'loading.method' has changed to "revised" in {EGAnet} version >= 2.0.7.
#> 
#>  For the previous default (version <= 2.0.6), use `loading.method = "original"`

# \donttest{
# Plot multilevel plot
plot(opt.hier, plot.type = "multilevel")


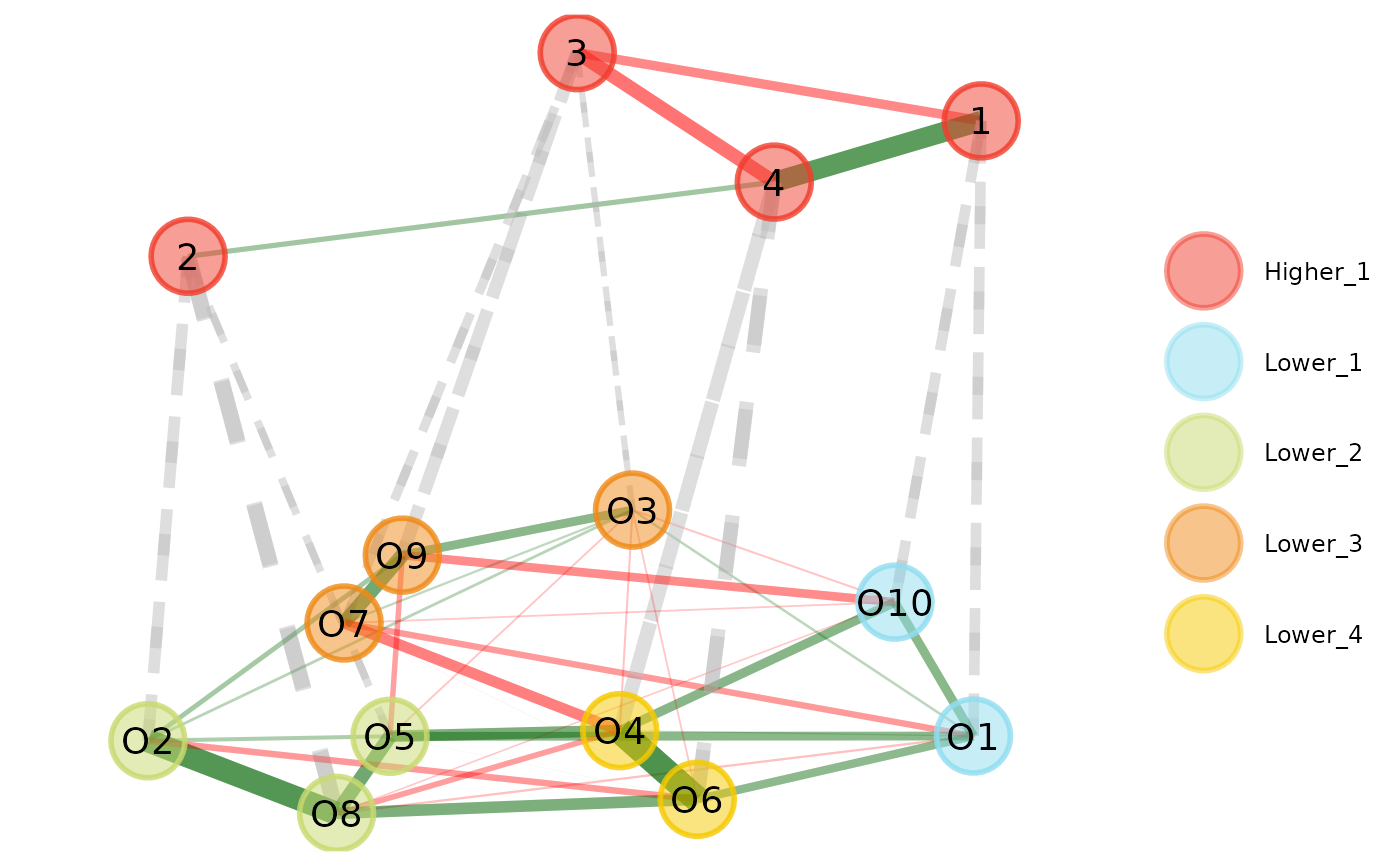# Plot multilevel plot with higher order
# border color matching the corresponding
# lower order color
plot(opt.hier, color.match = TRUE)



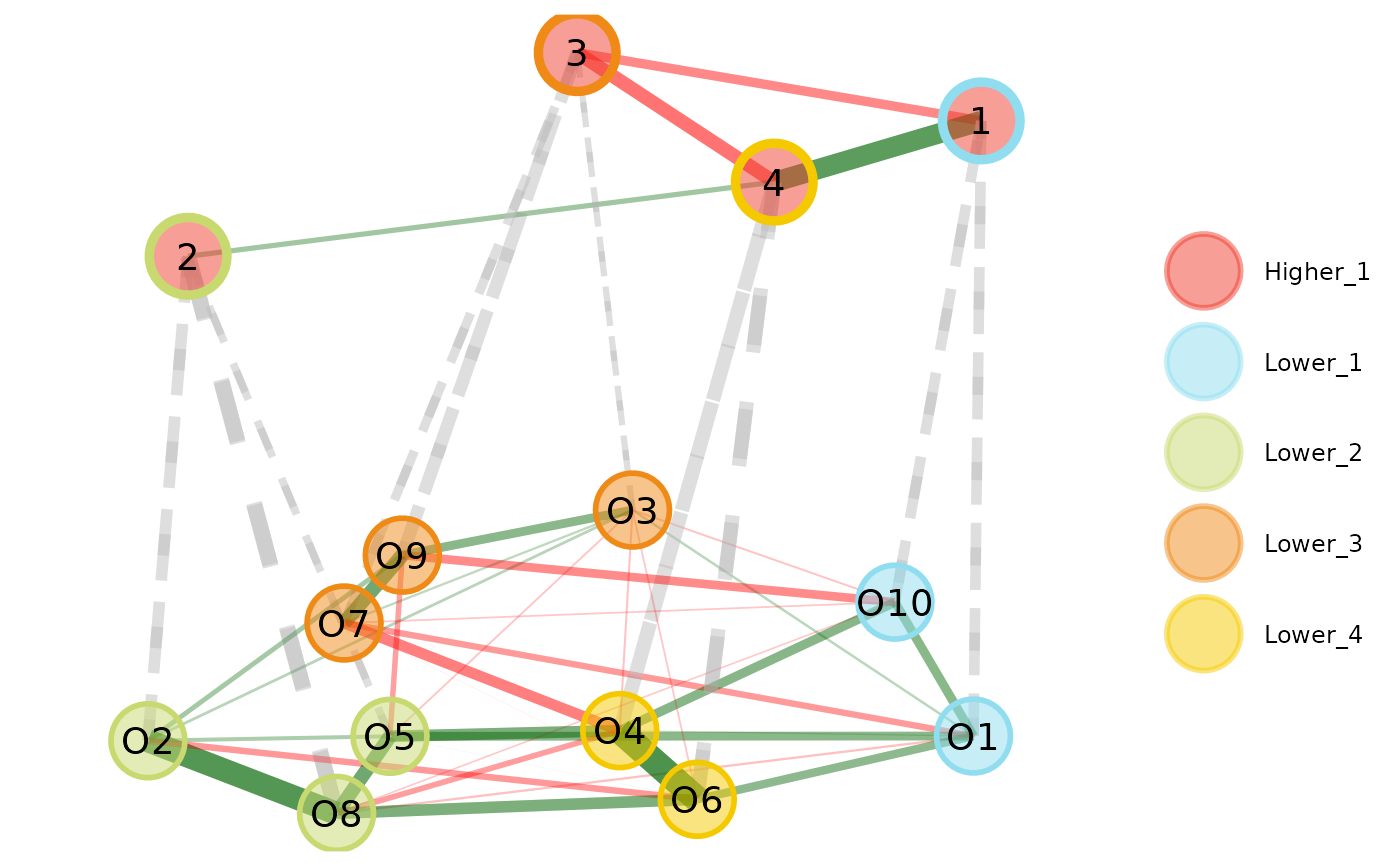
# Plot levels separately
plot(opt.hier, plot.type = "separate")# }